Unmasking Hidden Connections: The Power of Community Detection in Networks

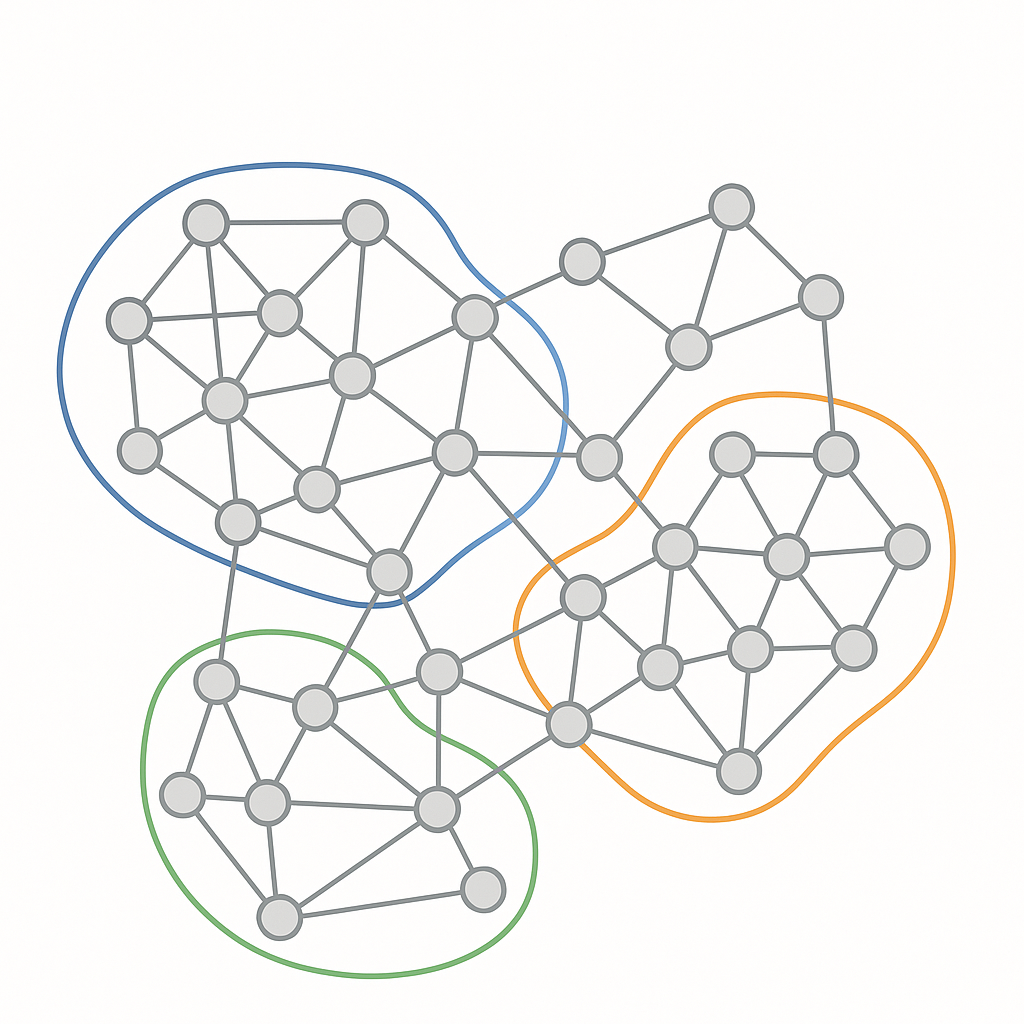
What are Communities in Networks?

Imagine a social network where individuals interact through friendships, professional ties, or family connections. Within such a network, you intuitively expect to observe various sub-structures: groups of friends who spend most of their time together, colleagues collaborating on a project, or family members forming a close-knit unit. These discernible groups, where members are more connected to each other than to individuals outside the group, are formally known as communities or clusters in a network.

More precisely, a community in a network is defined as a collection of nodes (or vertices) that exhibit a significantly higher density of internal connections (edges) among themselves compared to their connections with nodes belonging to other communities. Conversely, the connections between different communities are relatively sparse. This “dense internal, sparse external” characteristic is the fundamental principle underpinning most community detection efforts.

It’s important to note that the concept of a “community” can exist at various scales. A large organization might have broad departments (e.g., Engineering, Marketing), and within the Engineering department, there might be smaller project teams, and within those teams, even smaller informal groups of collaborators. All these can be considered communities at different levels of granularity. The challenge lies in developing algorithms that can effectively identify these structures without a predefined notion of their size or number. The precise definition of what constitutes a “community” can sometimes be ambiguous and depend on the context and the specific algorithm used.

Communities vs. Clusters: A Nuance

While “communities” and “clusters” are often used interchangeably in the context of network analysis, it’s worth noting a subtle distinction, particularly when comparing to broader data mining terminology.

• Clusters (General Data Mining): In the general field of data mining and machine learning, clustering refers to the task of grouping a set of objects in such a way that objects in the same group (a cluster) are more similar to each other than to those in other groups. This similarity is typically based on attribute values in a feature space. Algorithms like K-means, DBSCAN, or hierarchical clustering operate on data points in a multidimensional space.
• Communities (Network Analysis): In network analysis, “communities” specifically refer to groups of nodes that are densely connected within the group and sparsely connected outside the group. The grouping is explicitly based on the topology or structure of the graph, i.e., the presence and pattern of edges. While graph-based clustering algorithms exist, the term “community” emphasizes this structural connectivity aspect.

In essence, all communities are a type of cluster, but not all clusters (as defined in general data mining) are communities in a network sense, as they might not be defined by topological density. However, for practical purposes in network analysis, “community detection” and “graph clustering” are often synonymous.

Why is Community Detection Important?

The ability to identify and analyze community structures is not merely an academic exercise; it has profound practical implications across a multitude of disciplines. By revealing the inherent modular organization of complex systems, community detection offers valuable insights and enables better decision-making.

Here are some key application areas:

• Social Sciences and Sociology:
  • Application: Identifying social groups (e.g., friendship circles, political factions, online interest groups), opinion leaders, or “echo chambers” within social media.
  • Benefit: Helps sociologists understand social dynamics, influence propagation, group formation, and the spread of information or misinformation. For instance, detecting communities can reveal how social movements coalesce or how cultural trends emerge.
• Biology and Bioinformatics:
  • Application: Discovering protein complexes (groups of interacting proteins that perform specific functions), gene regulatory networks, metabolic pathways, or functional modules in biological systems.
  • Benefit: Crucial for understanding disease mechanisms, drug target identification, and developing new therapies. For example, if a specific community of genes is implicated in a disease, targeting multiple genes within that community might be more effective than targeting a single one.
• Computer Science and Data Mining:
  • Application: Understanding user behavior in online platforms (e.g., identifying user communities with similar preferences on e-commerce sites), detecting spam or bot communities, organizing information in knowledge graphs, or optimizing routing in communication networks.
  • Benefit: Leads to improved recommendation systems, enhanced cybersecurity (by flagging suspicious clusters of activity), more efficient data organization, and robust network design.
• Business and Economics:
  • Application: Identifying customer segments with similar purchasing habits or demographics, understanding supply chain vulnerabilities by detecting highly interdependent clusters of suppliers, or analyzing internal organizational structures.
  • Benefit: Enables targeted marketing campaigns, risk mitigation, and optimization of business processes. For example, a company might tailor product offerings or marketing messages specifically to identified customer communities.
• Finance and Fraud Detection:
  • Application: In financial networks, nodes might represent accounts, individuals, or transactions, and edges can represent money transfers, credit relationships, or shared attributes. Community detection can be highly effective in uncovering suspicious patterns.
  • Benefit: Helps financial institutions identify and prevent various types of fraud.
    • Credit Card Fraud Rings: Fraudsters often collaborate, sharing stolen card information or using the same point-of-sale terminals. Community detection can group together accounts that exhibit unusual spending patterns, share common transaction locations, or have links to known fraudulent entities, even if the direct links are sparse. A community of accounts with high velocities of transactions or unusual merchant categories could indicate a fraud ring.
    • Money Laundering: Money launderers move funds through complex networks of accounts to obscure the origin of illicit gains. Community detection can identify chains or clusters of transactions that appear to circulate money among a closed group of accounts without clear business justification, often involving multiple intermediaries. Unusual cyclic patterns of transactions within a detected community are strong indicators.
    • Insurance Fraud: Collusive insurance fraud involves multiple parties fabricating or exaggerating claims. By modeling individuals, service providers (e.g., auto repair shops, medical clinics), and claims as a network, communities of highly interconnected claims or individuals repeatedly involved in suspicious incidents can be flagged.
    • Loan Stacking/Application Fraud: Multiple fraudulent loan applications might originate from a small group, using slightly different identities or addresses but sharing underlying commonalities. Community detection on shared identifiers (e.g., phone numbers, IP addresses, physical addresses) can link these seemingly disparate applications into a single fraudulent cluster.
    • Insider Trading: In a network of stock traders and their transactions, suspicious communities might emerge where individuals consistently make similar trades just before major market announcements, indicating potential insider information sharing.

Types of Community Structures

Real-world networks can exhibit diverse community structures. Understanding these variations is essential for selecting appropriate detection algorithms and interpreting their results.

• Disjoint (or Non-Overlapping) Communities:
  • Description: In this simplest model, every node in the network belongs to exactly one community. The network is completely partitioned into mutually exclusive groups.
  • Analogy: Imagine a classroom where students are divided into several project groups, and each student is assigned to only one group.
  • Characteristics: Many classical community detection algorithms (including the basic Louvain method) inherently aim to find disjoint partitions. They are often suitable for scenarios where clear, separate divisions are expected or desired.
  • Examples: Departments in a traditional, rigidly structured organization, or distinct factions in a conflict where individuals must choose a side.
• Overlapping Communities:
  • Description: This structure is far more common in real-world networks. Here, a single node can be a member of multiple communities simultaneously.
  • Analogy: A person in a social network might belong to their family group, their work colleagues group, and a hobby club group.
  • Characteristics: Reflects the multifaceted nature of interactions in many systems. Algorithms designed for overlapping communities often leverage concepts like “cliques” (fully connected subgraphs) or “link communities” (where edges, rather than nodes, belong to communities).
  • Examples: An individual with diverse social circles, a gene participating in multiple biological pathways, or a research paper cited by multiple distinct research fields.
• Hierarchical Communities:
  • Description: In a hierarchical structure, communities are nested within larger communities, forming a multi-level organization. This suggests that a network can be viewed at different resolutions, revealing communities at coarse and fine granularities.
  • Analogy: A country divided into states/provinces, which are further divided into cities, and then into neighborhoods. Each level represents a community structure.
  • Characteristics: Many algorithms, including the Louvain method with its iterative aggregation phases, can naturally uncover hierarchical structures. By stopping the algorithm at different stages, one can explore communities at various levels of detail.
  • Examples: Organizational charts (where departments contain teams), biological classification (kingdoms, phyla, families, species), or linguistic structures (languages, dialects, sub-dialects).

Understanding these different types of community structures helps researchers choose the most appropriate algorithms and interpret the results in a meaningful way for their specific domain.

Next, I will delve into Modularity – Quantifying Community Quality, exploring why we need a metric to evaluate community structure and how modularity serves this purpose.